Eine Bandsperre filtert ein definiertes Frequenzband aus dem Signal heraus. Deshalb ist auch die Bezeichnung Kerbfilter geläufig. In diesem Artikel findest du verschiedene Schaltungsvarianten einer passiven Bandsperre. Neben den Formeln zur Berechnung des Sperrbandes enthält der Artikel praktische Online Rechner zur Unterstützung bei der Dimensionierung.
Allgemeine Infos zur Bandsperre
Die Bandsperre Schaltung oder der Bandstopp Filter ist eine elektrische Schaltung zum Ausfiltern von Frequenzen. Den Namen Bandsperre hat die Schaltung daher, dass sie ein Frequenzband abschwächt beziehungsweise sperrt. Frequenzen außerhalb dieses Bandes sollen mit möglichst wenig Verlust passieren. Passiv ist die Bandsperre, wenn keine verstärkenden Bauteile wie Transistoren in der Schaltung eingesetzt werden. Ist dies der Fall, handelt es sich um eine aktive Bandsperre.
Eine Einsatzmöglichkeit einer Bandsperre liegt in der Verbesserung der Signalübertragung. Hier könnte die Schaltung Signale eines bestimmten Frequenzbereiches herausfiltern, wenn diese unerwünscht sind und die Übertragung stören würden. Früher gab es den „Gebührenimpuls“ in der Telefonleitung, der Modems in ihrer Funktion behindern konnte. Mit einer passiven Bandsperre wurde dieser Impuls unterdrückt.
Eine passive Bandsperre besteht im Grunde aus der Parallelschaltung eines Hochpasses und eines Tiefpasses. Die Ordnung einer Bandsperre gibt dabei an, wie groß der Bereich des Frequenzübergangs ist. Dabei gilt: Je höher die Ordnung, desto kleiner dieser Übergangsbereich. Wir werden die Funktionsweise erklären und aufzeigen, wie sich eine Bandsperre berechnen lässt. Außerdem stellen wir einen Bandsperre Rechner zur Verfügung, der die Arbeit mit den Formeln erleichtert.
Passive Bandsperre 1. Ordnung
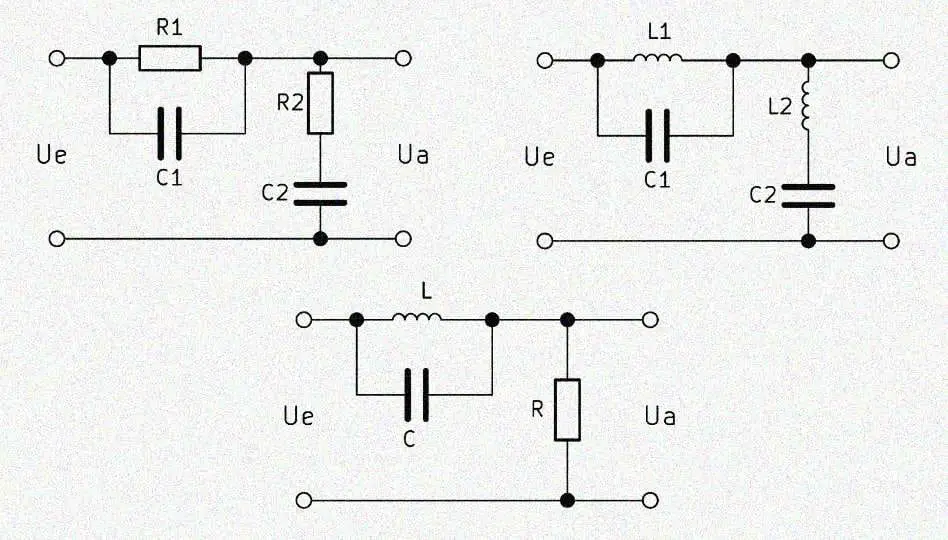
Eine Bandsperre 1. Ordnung entsteht im Prinzip durch die Parallelschaltung eines Hochpasses und eines Tiefpasses der 1. Ordnung. Es werden also zwei ohmsche Widerstände und zwei Kondensatoren benötigt, weshalb sich diese Schaltung auch RC Bandsperre nennt. Die Ausgangsspannung $U_a$ wird in der Mitte der beiden Schaltungen abgegriffen.
Mit Frequenz am Eingang verändert sich der Spannungsabfall über den beiden Schaltungen und somit das Verhältnis zwischen Eingangs- und Ausgangsspannung. Hohe Frequenzen passieren den Hochpassfilter und niedrige Frequenzen den Tiefpassfilter. Durch die Dimensionierung der Widerstände und Kondensatoren wird der Mittelbereich bestimmt, in dem nahezu keine Spannung am Ausgang ankommt.
RC Bandsperre – Funktionsweise
Die Bandsperre bedient sich der Vorteile von Hoch- und Tiefpass. Bei einer hohen Frequenz am Eingang fällt eine hohe Ausgangsspannung $U_a$ am Hochpass ab und bei einer niedrigen Eingangsfrequenz am Tiefpass. Durch die Parallelschaltung dieser beiden Elemente können hohe und niedrige Frequenzen fast ungehindert passieren.
In der Mitte ergibt sich ein von beiden Filtern überlagerter Bereich, in dem wenig Spannung am Ausgang abfällt. Die Eingangsspannung wird hier gleichzeitig vom Hochpass- und Tiefpassfilter abgeschwächt. Die Mitte dieses überlagerten Bereichs wird als Mittenfrequenz $f_0$ bezeichnet. Aufgrund der Charakteristik wird die Bandsperre auch manchmal als Badewannenfilter bezeichnet.
Formel – Bandsperre berechnen
Bei der einfachen RC Bandsperre sind in der Regel die Widerstände und Kondensatoren jeweils gleich groß. Die Bandsperre Übertragungsfunktion lautet in diesem Fall:
$$ A = \frac{1 – (\omega RC)^2}{1 + 4 \omega RC – (\omega RC)^2} $$
$R$ ist der ohmsche Widerstandswert und $C$ die Kapazität der Kondensatoren. Das $\omega$ ist die Kreisfrequenz aus $2 \cdot \pi \cdot f$.
Bandsperre Grenzfrequenz berechnen
Eine Bandsperre verfügt über zwei Grenzfrequenzen: Eine für den Hochpass und eine für den Tiefpass. Diese beiden Grenzfrequenzen werden getrennt berechnet. Sie ergeben sich beide aus dem Verhältnis:
$$ \frac{U_a}{U_e} = 70,7 \% $$
Neben den beiden Grenzfrequenzen ist zudem die Berechnung der Mittelfrequenz f0 interessant. Sie bildet den geometrischen Mittelwert aus der oberen Grenzfrequenz $f_{go}$ und der unteren Grenzfrequenz $f_{gu}$. Die Formel lautet:
$$ f_0 = \sqrt{f_{go} \cdot f_{gu}} $$
RC Bandsperre Rechner
Der Online Rechner hilft bei der Auslegung der Bauteile für die gewünschte Mittenfrequenz.
Bandsperre 2. Ordnung
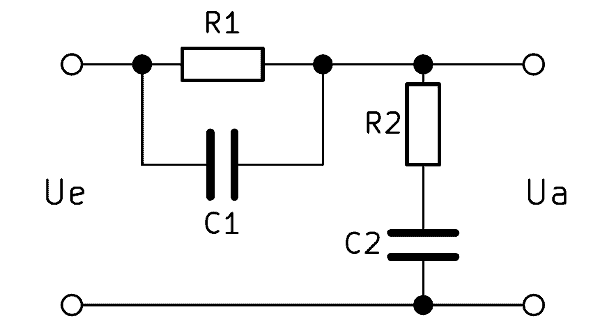
Ein Bandstopp Filter der 2. Ordnung wird identisch mit dem Filter der 1. Ordnung aufgebaut. Der Austausch des ohmschen Widerstands gegen eine Induktivität erhöht die Ordnung. Eine höhere Ordnung bedeutet, dass der Filtereffekt stärker wird und die Übergangsbereiche kleiner. Ein Filter 2. Ordnung weist eine doppelt so hohe Flankensteilheit auf wie ein Filter 1. Ordnung. Durch die Verschaltung weiterer Bandsperren kann die Ordnung auch noch weiter erhöht werden.
Funktionsweise LC Bandsperre
Wie der Aufbau ähnelt auch die Funktionsweise stark der Bandsperre Schaltung der 1. Ordnung. Die Induktivität jedoch besitzt ebenfalls einen Blindwiderstand $X_L$, der sich entgegengesetzt zum kapazitiven Blindwiderstand $X_C$ verhält. Das heißt: Bei einer steigenden Frequenz sinkt der Blindwiderstand des Kondensators und der Blindwiderstand der Spule erhöht sich gleichzeitig. Dadurch wird der Filtereffekt deutlich verstärkt und Frequenzänderungen am Eingang sind am Ausgang deutlicher zu sehen.
Formel – Bandsperre 2. Ordnung berechnen
Bei der LC Bandsperre gilt folgender Zusammenhang:
$$ Z = R_0 = \sqrt{\frac{L_1}{C_2}} = \sqrt{\frac{L_2}{C_1}} $$
Die Bandsperre Übertragungsfunktion der 2. Ordnung lautet:
$$ T(s) = \frac{1 + \frac{s^2}{\omega_0^2}}{1 + s \frac{B}{\omega_0^2} + \frac{s^2}{\omega_0^2}} $$
Grenzfrequenz LC Bandsperre berechnen
Auch hier gilt wieder, dass es eine untere und eine obere Grenzfrequenz gibt. Diese werden nach folgenden Formeln berechnet:
$$ f_{gu} = \frac{1}{2 \pi \sqrt{L_1 C_1} \left( -\frac{1}{2} \sqrt{\frac{C_2}{C_1}} + \sqrt{1 + \frac{1}{4} \frac{C_2}{C_1}} \right) } $$
$$ f_{go} = \frac{1}{2 \pi \sqrt{L_1 C_1} \left( +\frac{1}{2} \sqrt{\frac{C_2}{C_1}} + \sqrt{1 + \frac{1}{4} \frac{C_2}{C_1}} \right) } $$
LC Bandsperre Rechner
Der Online Rechner hilft bei der Auslegung der Bauteile zum Aufbau einer RC Bandsperre.
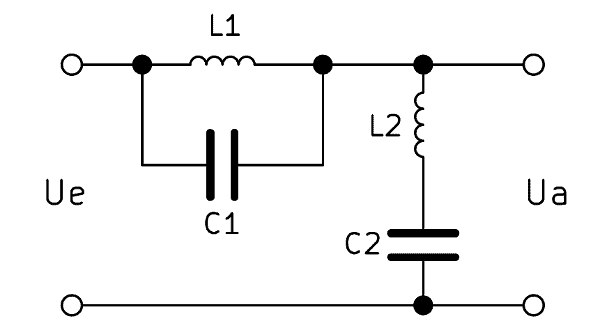
Alternative: RLC Bandsperre Schaltung
Eine Bandsperre der 2. Ordnung kann ebenfalls mit einer Schaltung aus Widerstand, Kondensator und Induktivität aufgebaut werden. Der Aufbau ist also identisch mit einem RLC Bandpass. Die Ausgangsspannung $U_a$ wird hier jedoch parallel zu Induktivität und Kondensator abgegriffen. Die Funktionsweise bleibt ebenfalls identisch, da sich die Blindwiderstände von Induktivität und Kondensator entgegengesetzt ändern.
Die Berechnung der $RLC$ Bandsperre erfolgt nach der Formel:
$$ \frac{U_a}{U_e} = \frac{1 – \frac{\omega^2}{\omega_2^2}}{1 – \frac{\omega^2}{\omega_2^2} + j \frac{\omega}{\omega_1}} $$