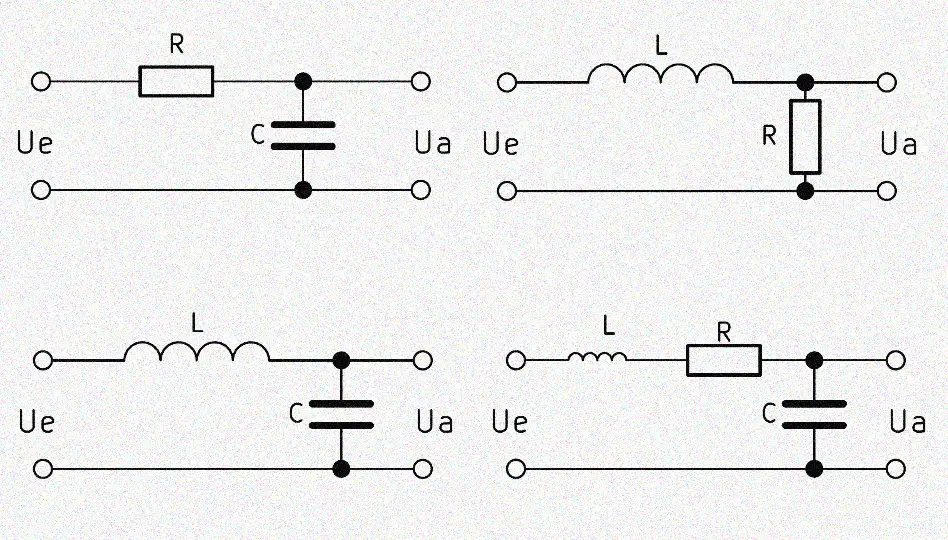
Ein Tiefpass Filter lässt nur Signale unterhalb seiner Grenzfrequenz durch und schwächt die Anteile darüber ab. Hier erfährst du, wie du die verschiedenen Varianten eines passiven Tiefpass Filters berechnen kannst. Neben den Formeln stehen mehrere Tiefpass Rechner zur Hilfe bereit.
Allgemeines Infos zum Tiefpass Filter
Ein Tiefpass bezeichnet in der Elektrotechnik eine Komponente, die hohe Frequenzen abschwächt beziehungsweise sperrt und niedrige Frequenzen weitestgehend ungehindert passieren lässt. Auch die Bezeichnung Tiefpassfilter ist geläufig. Der Begriff passiv bedeutet dabei lediglich, dass die Schaltung ohne ein verstärkendes Element aufgebaut wird. Bei der Verwendung eines Operationsverstärkers hätten wir einen aktiven Tiefpass.
Einsatzbereiche eines Tiefpasses liegen dort, wo schnelle und sprunghafte Spannungsänderungen am Ausgang unerwünscht sind. Er kommt beispielsweise beim Bau von Tieftonlautsprechern zum Einsatz, um deren Akustik zu verbessern. Auch bei Netzfiltern wird häufig ein Tiefpass eingesetzt, um aus dem Stromnetz übertragene, hohe Störfrequenzen zu entfernen.
Fachleute unterscheiden den Tiefpass 1. Ordnung und den Tiefpass 2. Ordnung. Wir erklären, aus welchen Elementen der jeweilige Tiefpass besteht, wie er funktioniert und wie sich ein Tiefpassfilter berechnen lässt. Da es sich hier um recht komplexe Rechnungen handelt, stellen wir außerdem einen Tiefpass Rechner zur Verfügung.
Passiver Tiefpass 1. Ordnung
Der Tiefpass 1. Ordnung besteht aus einem Widerstand und einem dazu in Reihe geschalteten Kondensator. Deshalb ist auch die Bezeichnung RC Tiefpass geläufig, wobei das $R$ für den Widerstand und das $C$ für den Kondensator steht. Parallel zum Kondensator wird die Ausgangsspannung $U_a$ abgegriffen. Das ist wichtig, weil es sich andernfalls um einen Hochpassfilter handelt.
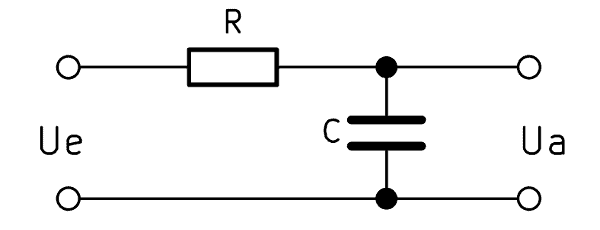
Bei schnellen Änderungen der Eingangsspannung $U_e$ fällt am Kondensator nahezu keine Spannung ab, wodurch sich auch die Ausgangsspannung $U_a$ nahe 0 bewegt. Kommt es hingegen zu einer langsamen Änderung der Spannung $U_e$, fällt ein Teil der Spannung über dem Kondensator ab. Die Ausgangsspannung $U_a$ verändert sich mit einer zeitlichen Verzögerung. Im folgenden Abschnitt wollen wir einen RC Tiefpass berechnen und die Funktionsweise näher beleuchten.
RC Tiefpass – Funktionsweise
Die Ausgangsspannung $U_a$ folgt der sprunghaft geänderten Eingangsspannung $U_e$ zeitlich verzögert in der gleichen Sprunghöhe. Das liegt daran, dass die veränderte Eingangsspannung den Kondensator kurzzeitig passiert, weil sich der kapazitive Widerstand des Kondensators erst aufbaut. Hat der kapazitive Blindwiderstand seinen neuen Wert erreicht, verändert sich auch die Ausgangsspannung nicht weiter.
Bei einer sinusförmigen Eingangsspannung hingegen erhalten wir eine abgeschwächte Ausgangsspannung. Die Abschwächung hängt dabei durch den sich langsam aufbauenden kapazitiven Blindwiderstand des Kondensators stark von der Frequenz ab. Mit steigender Eingangsfrequenz steigt auch die Differenz zwischen Eingangs- und Ausgangsspannung.
Formel – Tiefpassfilter berechnen
Die Formel zur Berechnung eines RC Tiefpasses lautet:
$$ \frac{U_a}{U_e} = \frac{1}{\sqrt{1 + (ωCR)^2}} $$
Hierbei steht $U_e$ für die Eingangsspannung und $U_a$ für die Ausgangsspannung. Das $\omega$ ist die Kreisfrequenz, also das Produkt aus $2 \cdot \pi \cdot f$ (Frequenz). $C$ ist die Kapazität des Kondensators und $R$ der ohmsche Widerstandswert.
Grenzfrequenz Tiefpass berechnen
Der ohmsche Widerstand $R$ bleibt unverändert, während sich der kapazitive Blindwiderstand $X_C$ in Abhängigkeit von der Frequenz ändert. Die Grenzfrequenz bezeichnet die Frequenz, bei der die beiden Werte gleich groß sind, also $R = X_C$. Bei einer Frequenz über der Grenzfrequenz ist folglich $X_C$ kleiner als $R$, bei einer niedrigeren Frequenz ist $X_C$ größer als $R$. Beim Betrieb mit der Grenzfrequenz kommen 70,71% der Eingangsspannung am Ausgang an, bedingt durch den Scheitelfaktor $\sqrt{2}$.
Die Berechnung der Grenzfrequenz bei einem RC Tiefpass erfolg nach dieser Formel:
$$ f_g = \frac{1}{2 \pi R C} $$
RC Tiefpass Rechner
Mit dem Online Rechner kannst du die benötigten Bauteile für die gewünschte Grenzfrequenz berechnen.
Alternative: RL Tiefpass
Wenn anstelle des Kondensators eine Spule verwendet wird, kann ebenfalls ein Tiefpass der 1. Ordnung aufgebaut werden. Hierzu muss die Ausgangsspannung jedoch parallel zum Widerstand abgegriffen werden. Die Funktionsweise ist hier genau umgekehrt: Je höher die Frequenz, umso größer ist der Anteil der Spannung, welche über der Spule abfällt.
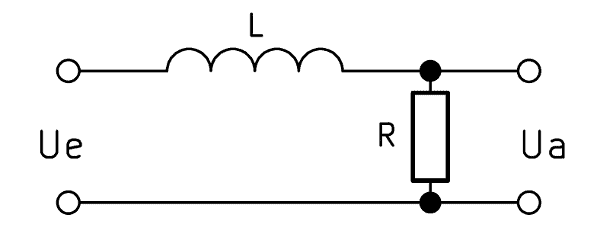
Die Formel für die Berechnung der Ausgangsspannung lautet dann:
$$ \frac{U_a}{U_e} = \frac{1}{\sqrt{1+ (\omega \frac{L}{R})^2}} $$
Die Grenzfrequenz kann bei einem LR-Tiefpass mit dieser Formel ermittelt werden:
$$ f_g = \frac{R}{2 \pi L} $$
RL Tiefpass Rechner
Der Online Rechner hilft dir bei der Berechnung der benötigten Bauteile für die gewünschte Grenzfrequenz.
Passiver Tiefpass 2. Ordnung
Der Tiefpass 2. Ordnung besteht ebenfalls aus zwei Bauteilen. Eine Spule wird mit einem Kondensator in Reihe geschaltet, weshalb dieser Tiefpass auch als LC Tiefpass bezeichnet wird. Auch hier wird parallel zum Kondensator die Ausgangsspannung $U_a$ abgegriffen. Der Aufbau ist also identisch zum Tiefpass 1. Ordnung, es wird nur der ohmsche Widerstand gegen eine Spule ausgetauscht.
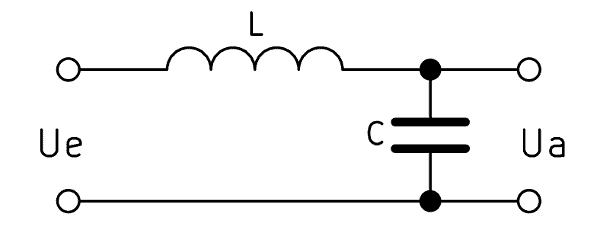
Ein Tiefpass 2. Ordnung erfüllt im Grunde die gleiche Funktion wie sein Verwandter 1. Ordnung, verfügt jedoch über eine doppelt so hohe Flankensteilheit.
Niedrige Frequenzen können also passieren, während hohe Frequenzen doppelt so effektiv gefiltert werden. Den Unterschied verursacht die Spule. Sie reagiert als induktiver Verbraucher viel schneller auf Spannungsänderungen als ein ohmscher Widerstand.
LC Tiefpass – Funktionsweise
Die Funktion des Kondensators ist genau die gleiche wie beim Tiefpass 1. Ordnung. Er befindet sich genau an der gleichen Stelle und auch die Ausgangsspannung wird identisch abgegriffen. Die Reaktion auf eine einzelne, sprunghafte Änderung der Eingangsspannung ist ebenfalls vergleichbar. Die Spule hat einen Widerstand nahe Null, solange eine Gleichspannung angelegt wird.
Der Unterschied zeigt sich erst beim Anlegen einer sich ändernden Spannung. Die Spule reagiert stärker auf die Erhöhung der Frequenz als ein ohmscher Widerstand. Mit steigender Frequenz erhöht sich der induktive Blindwiderstand der Spule $X_L$, während der kapazitive Widerstand $X_C$ des Kondensators abnimmt. Somit spiegeln sich Veränderungen der Frequenz am Eingang noch deutlicher in der Höhe der Ausgangsspannung wieder.
Formel – Tiefpass 2. Ordnung berechnen
Die Formel zur Berechnung des LC Tiefpasses lautet:
$$ \frac{U_a}{U_e} = \frac{1}{1 – \omega^2 LC} $$
Bei der Berechnung kommt nun $L$ hinzu, die Induktivität der Spule. Dafür fällt der ohmsche Widerstand $R$ weg. Zur einfachen Berechnung des Tiefpasses stellen wir einen LC Tiefpass Rechner zur Verfügung.
Grenzfrequenz beim LC Tiefpass berechnen
Der induktive Widerstand $X_L$ steigt mit der Frequenz, während sich der kapazitive Blindwiderstand $X_C$ bei steigender Frequenz verringert. Die Grenzfrequenz bezeichnet die Frequenz, bei der gilt: $X_C = X_L$. Bei einer Frequenz größer der Grenzfrequenz ist folglich $X_C$ kleiner als $X_L$. Bei einer niedrigeren Frequenz ist $X_C$ größer als $X_L$.
Die Grenzfrequenz bei einem LC Tiefpass wird nach der folgenden Formel berechnet:
$$ f_g = \frac{1}{2 \pi \sqrt{LC}} $$
LC Tiefpass Rechner
Hier kannst du die gewünschte Grenzfrequenz sowie die dafür benötigten Bauteile berechnen.