Ein Hochpass Filter hindert Frequenzen unterhalb seiner Grenzfrequenz und lässt Signale überhalb passieren. In diesem Artikel erfährst du, wie die verschiedenen passiven Hochpass Filter berechnet werden. Neben den Formeln helfen die Online Rechner dabei.
Allgemeine Infos zum Hochpass Filter
Ein Hochpass benennt in der Elektrotechnik eine Schaltung mit dem Zweck, tiefe Frequenzen abzuschwächen oder zu sperren. Hohe Frequenzen hingegen sollen möglichst ungehindert passieren. Der Begriff Hochpassfilter ist ebenfalls geläufig. Der Hochpass ist passiv, wenn kein verstärkendes Element eingesetzt wird, andernfalls wäre er aktiv.
Ein Hochpass wird dort eingesetzt, wo tiefe Frequenzen unerwünscht sind und deshalb herausgefiltert werden sollen. Beispiele sind der Bau von Hochtonlautsprechern oder die hochfrequente Signalübertragung über Stromleitungen. Die tiefen Frequenzen würden in diesen Fällen das Signal für die weitere Verarbeitung nahezu unbrauchbar machen und müssen beseitigt werden.
Elektrofachmänner unterscheiden zwischen einem Hochpass 1. Ordnung und 2. Ordnung. Hochpässe höherer Ordnung werden durch das in Reihe schalten niedrigerer Ordnungen erreicht. Wir erklären, wie der Hochpass funktioniert und wie sich ein Hochpass berechnen lässt. Außerdem stellen wir zur Vereinfachung einen Hochpass Rechner zur Verfügung.
Passiver Hochpass 1. Ordnung
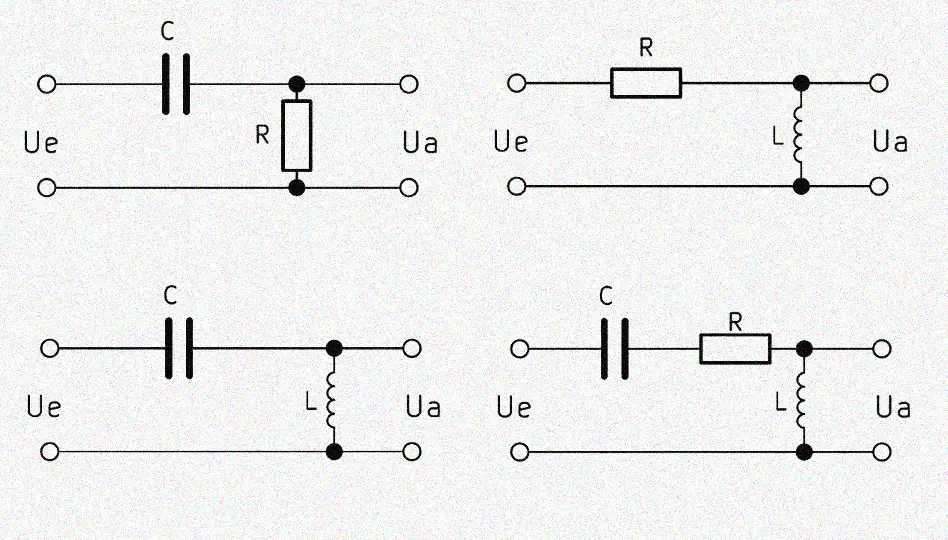
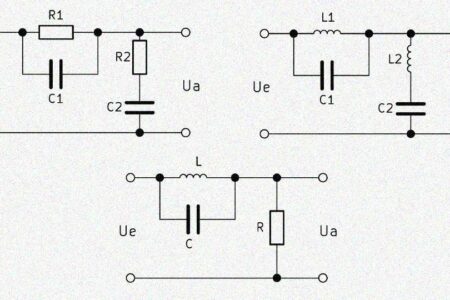
Der einfache Hochpass der 1. Ordnung wird mit einem Kondensator und einem in Reihe geschalteten Widerstand aufgebaut. Der Kondensator trägt die Abkürzung $C$ und der Widerstand $R$, weshalb häufig die Kurzbezeichnung $RC$ Hochpass verwendet wird. Ein $CR$ Hochpass wird ebenfalls oft genannt, bezeichnet aber die gleiche Schaltung. Die Ausgangsspannung $U_a$ muss hier parallel zum Widerstand abgegriffen werden, da wir andernfalls einen Tiefpassfilter erhalten.
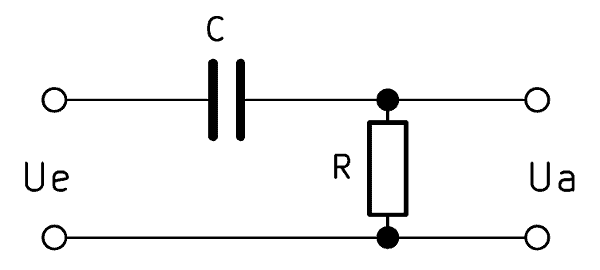
Wenn am Eingang eine hohe Frequenz angelegt wird, fällt am Kondensator eine unmerklich kleine Spannung ab. Die Ausgangsspannung $U_a$ ist somit fast identisch mit der Eingangsspannung $U_e$. Liegt jedoch eine niedrige Frequenz an, fällt ein Teil der Spannung über dem Kondensator ab. In der Folge sinkt die Ausgangsspannung parallel zum Widerstand mit einer zeitlichen Verzögerung.
RC Hochpass – Funktionsweise
Bei einer einzelnen, sprunghaften Änderung der Eingangsspannung $U_e$ gibt es eine kurze Spannungsspitze der Ausgangsspannung $U_a$. Das kommt daher, dass der Kondensator die veränderte Spannung kurzzeitig passieren lässt. Sein kapazitiver Blindwiderstand $X_C$ braucht eine kurze Zeit, bis er sich aufbaut.
Besitzt die Eingangsspannung allerdings eine Frequenz, hängt $X_C$ von der Höhe dieser Frequenz ab. Mit steigender Frequenz sinkt der Spannungsabfall über dem Kondensator. Folglich steigt die Ausgangsspannung. Bei einer niedrigen Frequenz vergrößert sich $X_C$ und es fällt mehr Spannung über dem Kondensator ab. Die Ausgangsspannung $U_a$ sinkt.
Formel – Hochpassfilter berechnen
Die Grundformel zur Berechnung eines RC Hochpass lautet:
$$ \frac{U_a}{U_e} = \frac{R}{Z} $$
Dabei gilt für die Impedanz Z:
$$ Z = \sqrt{R^2 + X_C^2} $$
Die RC Hochpass Übertragungsfunktion ist:
$$ \frac{U_a}{U_e} = \frac{1}{\sqrt{1 + \frac{1}{(2 \pi f R C)^2}}} $$
$R$ steht für den ohmschen Widerstand. $f$ ist die Frequenz und $C$ die Kapazität des Kondensators.
Grenzfrequenz Hochpass berechnen
Der kapazitive Blindwiderstand $X_C$ sinkt bei steigender Frequenz, während der ohmsche Widerstand $R$ konstant bleibt. Die Grenzfrequenz $f_g$ ist die Frequenz, bei welcher die Widerstände gleich groß sind. Bei einer Frequenz oberhalb von $f_g$ ist folglich $R > X_C$ und bei einer niedrigeren Frequenz $X_C > R$.
Mit dieser Formel lässt sich die Grenzfrequenz bei einem RC Hochpass berechnen:
$$ f_g = \frac{1}{2 \pi R C} $$
RC Hochpass Rechner
Der Online Rechner hilft dir bei der Dimensionierung der Bauteile für die gewünschte Grenzfrequenz.
Alternative: RL Hochpass
Beim RL Hochpass handelt es sich ebenfalls um einen Filter der 1. Ordnung. Anstelle des Kondensators wird jedoch eine Induktivität eingesetzt und die Ausgangsspannung parallel zu dieser abgegriffen. Die Funktionsweise ist exakt umgekehrt: Der induktive Blindwiderstand $X_L$ steigt zusammen mit der Frequenz.
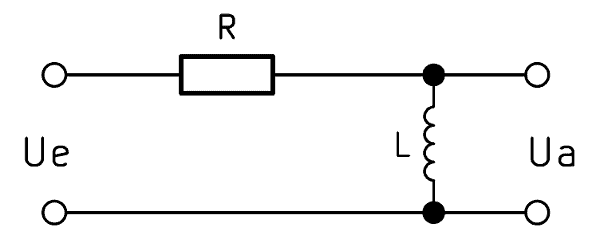
Die Formel zur Berechnung lautet dann:
$$ \frac{U_a}{U_e} = \frac{1}{\sqrt{1 + (2 \pi f L)^2}} $$
Die Grenzfrequenz bei einem RL Hochpass ergibt sich aus:
$$ f_g = \frac{R}{2 \pi L} $$
RL Hochpass Rechner
Der Online Rechner hilft dir bei der Dimensionierung der Bauteile für die gewünschte Grenzfrequenz.
Passiver Hochpass 2. Ordnung
Der Aufbau ist identisch mit dem Hochpassfilter 1. Ordnung, nur dass der ohmsche Widerstand gegen eine Induktivität ausgetauscht wird. Folglich wird beim Hochpass 2. Ordnung eine Spule mit einem Kondensator in Reihe geschaltet. Die Bezeichnung LC Hochpass ist deshalb geläufig. Die Ausgangsspannung $U_a$ wird hier über der induktiven Last abgegriffen.
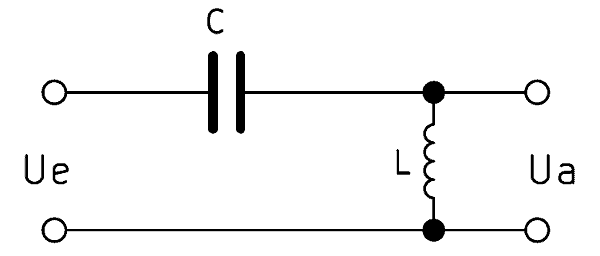
Ein Hochpass 2. Ordnung filtert die tiefen Frequenzen doppelt so effektiv wie ein Hochpass 1. Ordnung. Man spricht von einer doppelt so hohen Flankensteilheit. Der Unterschied kommt durch die Spule, die im Gegensatz zum Kondensator schnell auf hohe Frequenzen reagiert.
LC Hochpass Funktionsweise
Die Funktion des Kondensators bleibt unverändert. Bei einer niederfrequenten Eingangsspannung bildet er einen hohen kapazitiven Blindwiderstand $X_C$. Eine sprunghafte Änderung bewirkt daher eine kurzzeitige Spannungsspitze am Ausgang, weil der Kondensator verzögert reagiert.
Beim Anlegen einer Sinusspannung jedoch erfüllt die Spule ihren Zweck. Der Kondensator bildet einen Widerstand bei niedrigen Frequenzen und lässt hohe Frequenzen durch. Die Spule hingegen reagiert sofort auf einen Anstieg der Frequenz und bildet einen induktiven Blindwiderstand $X_L$. Im Gegensatz zum Kondensator steigt ihr Widerstand also gemeinsam mit der Frequenz. Das sorgt für eine schnellere und stärkere Reaktion auf Frequenzerhöhungen.
Formel – Hochpass 2. Ordnung berechnen
Die Formel zur Berechnung eines LC Hochpass lauten:
$$ L = \frac{Z}{2 \pi f} $$
$$ C = \frac{1}{2 \pi f Z} $$
$$ f = \frac{1}{2 \pi \sqrt{LC}} $$
$$ Z = \sqrt{\frac{L}{C}} $$
Die zugehörige Hochpass Übertragungsfunktion lautet:
$$ \frac{U_a}{U_e} = \frac{X_L}{X_L + X_C} $$
$L$ steht für die Induktivität der Spule, $Z$ für die Impedanz und $C$ für die Kapazität des Kondensators.
Grenzfrequenz Hochpass 2. Ordnung berechnen
Wie oben beschrieben verändern sich kapazitiver und induktiver Blindwiderstand immer in entgegengesetzter Richtung. Bei der Grenzfrequenz sind die Widerstände identisch. Es gilt also: $X_L = X_C$. Bei einer höheren Frequenz ist folglich $X_C > X_L$ und bei einer niedrigeren Frequenz $X_C < X_L$.
Die Formel zur Berechnung der Grenzfrequenz lautet:
$$ f_g = \frac{1}{2 \pi \sqrt{LC}} $$
LC Hochpass Rechner
Der Online Rechner hilft dir bei der Dimensionierung der Bauteile für die gewünschte Grenzfrequenz.