Ein Bandpass Filter lässt nur ein bestimmtes Frequenzband passieren und schwächt Frequenzen unter- und oberhalb ab. Dieser Artikel zeigt dir verschiedene Schaltungsvarianten von passiven Bandpassfiltern. Neben den Formeln findest du praktische Bandpass Rechner zur einfachen Berechnung des Filters.
Allgemeine Infos zum Bandpass Filter
Eine Bandpass Schaltung oder ein Bandpassfilter bezeichnet eine Komponente zur Filterung von Frequenzen. Der Name „Bandpass“ kommt daher, dass der Filter ein bestimmtes Frequenzband passieren lässt. Er schwächt also die Frequenzen oberhalb und unterhalb des Frequenzbandes ab. Der Bandpass besteht in seiner einfachsten Form aus einer Kombination von Hochpass- und Tiefpassfilter.
Ein Bandpass kommt beispielsweise im Lautsprecherbau zum Einsatz. Er könnte dort das Frequenzband des Mitteltonlautsprechers begrenzen. Das sorgt für einen verbesserten Klang, weil alle Frequenzen außerhalb eines bestimmten Bereichs vom Lautsprecher nicht sauber wiedergegeben werden können. Ein weiteres Anwendungsbeispiel sind Empfänger von Funksignalen, die mit dem Bandpass auf einen Empfangsbereich beschränkt werden.
Beim Bandpass gibt es aktive und passive Filter. Eine passive Bandpass Schaltung liegt vor, wenn kein verstärkendes Element eingesetzt wird. Der Bandpass kann in verschiedenen Ordnungen ausgeführt sein, wobei der Bandpass 1. Ordnung die Grundvariante bildet. Wir erklären die Funktionsweise des Bandpasses und erläutern, wie sich ein Bandpass Filter berechnen lässt. Zudem senkt unser Bandpass Rechner den Aufwand bei der Berechnung. Damit stellt das Bandpass Filter selber bauen kein Problem mehr dar.
Passiver Bandpass 1. Ordnung
Der einfache Bandpass besteht aus einem RC-Tiefpass und einem RC-Hochpass jeweils 1. Ordnung, also zwei Widerständen und zwei Kondensatoren. Hoch- und Tiefpassfilter werden hier einfach hintereinander geschaltet. Die Ausgangsspannung $U_a$ wird hinter beiden Filtern abgegriffen. Diese Variante wird auch als RC Bandpass bezeichnet.
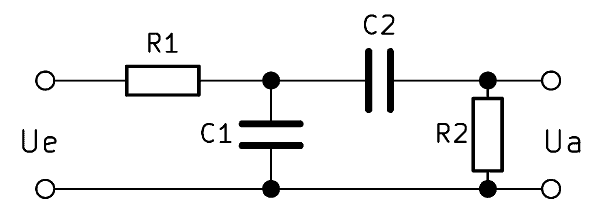
Wird am Eingang eine niedrige Frequenz angelegt, fällt ein Teil der Spannung über dem Hochpassfilter ab. Liegt eine hohe Frequenz an, fällt die Spannung über dem Tiefpassfilter ab. Bei einer mittleren Frequenz dringt der größte Teil der Eingangsspannung $U_e$ bis zum Ausgang durch. Die Frequenz der Eingangsspannung bestimmt also maßgeblich die Höhe der Ausgangsspannung.
RC Bandpass – Funktionsweise
Der RC Bandpass funktioniert durch die Zusammensetzung aus Hochpass- und Tiefpassfilter genau so wie diese beiden Elemente. Im Hochpassteil wird die Spannung über dem Widerstand abgegriffen, beim Tiefpass über dem Kondensator. Die parallel zu diesen beiden Komponenten abgegriffene Ausgangsspannung $U_a$ steigt, wenn sich die Eingangsfrequenz der Mittelfrequenz nähert. Durch das Verhältnis der Widerstände zu den Kondensatoren kann somit das Frequenzband bestimmt werden, welches der Filter durchlässt.
Formel – Bandpass berechnen online
Normalerweise werden bei einem Bandpass zwei gleiche Widerstände und zwei gleiche Kondensatoren ausgewählt. Wenn dies der Fall ist, dann gilt die Bandpass Übertragungsfunktion:
$$ \frac{U_a}{U_e} = \frac{1}{3 + j \left( \omega R C – \frac{1}{\omega R C} \right)} $$
$\omega$ ist die Kreisfrequenz aus $2 \cdot \pi \cdot f$. $R$ ist der Widerstandswert und $C$ die Kapazität des Kondensators. Mithilfe dieser Formel lässt sich ein Bandpass berechnen.
Grenzfrequenz Bandpass berechnen
Mit der Frequenz verändern sich die Widerstände von Hoch- und Tiefpass jeweils in entgegengesetzter Richtung. Das heißt: Steigt der Widerstand des Hochpasses, fällt gleichzeitig der des Tiefpasses. Die Grenzfrequenzen beider Filter werden getrennt berechnet und mit $f_H$ (high) und $f_L$ (low) bezeichnet. Mit diesen beiden Grenzfrequenzen lassen sich anschließend die Mittenfrequenz $\mathbf{f_0}$ und die Bandbreite $\mathbf{B}$ des gesamten Filters ermitteln.
Die Formel zur Berechnung der Frequenzen lautet:
$$ f_0 = \frac{1}{2 \pi RC} $$
$$ f_0 = \sqrt{f_H \cdot f_L} $$
$$ B = f_H – f_L $$
RC Bandpass Rechner
Der RC Bandpass Rechner erleichtert die Arbeit für alle, die einen Bandpass Filter selber bauen wollen.
Alternative: LC Bandpass der 1. Ordnung
Der sogenannte Butterworthfilter besteht einfach nur aus einer Induktivität, mit der eine Kapazität in Reihe geschaltet wird. Dies ist die einfachste Variante, einen Bandpassfilter aufzubauen. Die beiden Bauteile filtern sehr hohe und sehr niedrige Frequenzen aus.
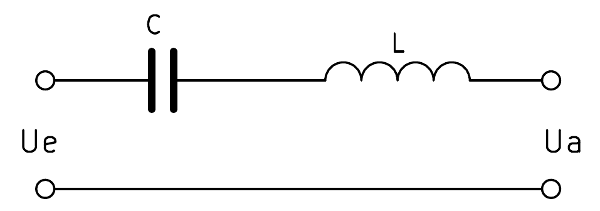
Die Formeln zur Berechnung von Spule und Kondensator lauten:
$$ C = \frac{1}{2 \pi \cdot Z \cdot f_L} $$
$$ L = \frac{Z}{2 \pi \cdot f_H} $$
Passiver Bandpass 2. Ordnung
Ein Bandpass der 2. Ordnung wird meist mit einer Schaltung aus zwei Kapazitäten und zwei Induktivitäten aufgebaut. Dabei ist die Verschaltung identisch zum RC Bandpass 1. Ordnung, es werden lediglich die Widerstände gegen Induktivitäten ausgetauscht. Der Filtereffekt verstärkt sich dadurch.
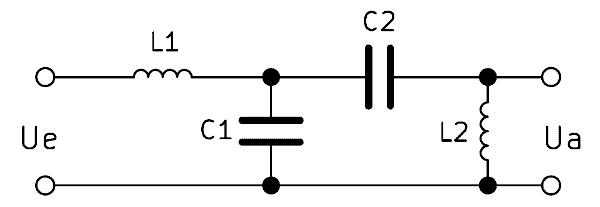
Der Bandpassfilter 2. Ordnung weist eine doppelt so hohe Flankensteilheit wie ein Filter der 1. Ordnung auf. Das bedeutet, dass er bei Änderungen der Frequenz doppelt so stark reagiert und folglich stärker filtert. Durch die Reihenschaltung mehrerer Bandpässe kann die Ordnung bei Bedarf noch weiter erhöht werden.
LC Bandpass Funktionsweise
Durch den Austausch der Widerstände gegen Induktivitäten erhöht sich die Flankensteilheit. Widerstände besitzen frequenzunabhängig immer den gleichen Widerstandswert. Der Grund für die Veränderung ist, dass die Induktivität deutlich schneller auf die Änderung der Frequenz reagieren. Mit einer Erhöhung der Frequenz steigen die induktiven Blindwiderstände $X_L$ der Induktivitäten.
Formel – Bandpass 2. Ordnung berechnen
Für das Verhältnis der Kapazitäten und Induktivitäten gilt:
$$ Z = R_0 = \sqrt{\frac{L_1}{C_2}} = \sqrt{\frac{L_2}{C_2}} $$
$L$ bezeichnet die Induktivität und $C$ die Kapazität des Kondensators.
Grenzfrequenz Bandpass der 2. Ordnung berechnen
Auch hier verändern sich der kapazitive und induktive Blindwiderstand in die jeweils entgegengesetzte Richtung. Die Grenzfrequenz ist die Frequenz, bei welcher die beiden Widerstandswerte identisch sind. Steigt die Frequenz weiter, ist $X_L$ größer und $X_C$ wird kleiner.
Die Formel für die obere und untere Grenzfrequenz lauten:
$$ f_{go} = \frac{1}{2 \pi \sqrt{L_1 C_1} \left( -\frac{1}{2} \sqrt{\frac{C_1}{C_2}} + \sqrt{1 + \frac{1}{4} \frac{C_1}{C_2}} \right) } $$
$$ f_{gu} = \frac{1}{2 \pi \sqrt{L_1 C_1} \left( +\frac{1}{2} \sqrt{\frac{C_1}{C_2}} + \sqrt{1 + \frac{1}{4} \frac{C_1}{C_2}} \right) } $$
LC Bandpass Rechner
Der LC Bandpass Rechner hilft bei der Dimensionierung der Bauteile anhand der benötigten Grenzfrequenzen.
Alternativ: RLC Bandpass
Ein Bandpass der 2. Ordnung kann auch mit drei in Reihe geschalteten Bauteilen aufgebaut werden: eine Induktivität, eine Kapazität und ein Widerstand. Die Ausgangsspannung $U_a$ wird hier parallel zum Widerstand abgegriffen. Die Funktionsweise ist ähnlich dem Bandpass mit Widerständen und Kondensatoren. Der induktive Blindwiderstand $X_L$ steigt zusammen mit der Frequenz, während sich $X_C$ umgekehrt verhält.

Die Bandpass Übertragungsfunktion lautet dann:
$$ \frac{U_a}{U_e} = \frac{1}{\frac{LC}{s^2 + s \frac{1}{RC} + \frac{1}{LC}}} $$
Die Grenzfrequenz des RLC Bandpass wird folgendermaßen berechnet:
$$ f_0 = \frac{1}{2 \pi \sqrt{LC}} $$