A smoothing capacitor reduces the residual ripple of a previously rectified voltage. This article describes the operation of a smoothing capacitor. In addition to the calculation formula, you will also find a practical online calculator for sizing the capacitor.
General information about the smoothing capacitor
The German power grid supplies a sinusoidal AC voltage with a frequency of 50 Hz. However, many devices are operated with a DC voltage. When connecting these devices, the voltage must be rectified in advance. Most commonly, the rectifier circuit is constructed with a bridge rectifier consisting of four diodes. However, this circuit has a big disadvantage: It works only from the lower half-wave upwards and leaves a pulsating DC voltage. Experts speak of a high ripple.
A smoothing capacitor, also called a filter capacitor or charging capacitor, is used to “smooth” these voltages. It weakens the ripple. Although the capacitor does not produce perfect DC voltage, it reduces the fluctuations to a level that most devices can easily handle. The remaining ripple is called the ripple voltage.
For a voltage with as little residual ripple as possible, the capacitor must be the right size. However, it may not be infinitely large, as the diodes could be damaged. We want to explain how a smoothing capacitor can be dimensioned and how exactly it works. Our online filter capacitor calculator helps with dimensioning the capacity.
Function of the smoothing capacitor
The capacitor for voltage smoothing is placed parallel to the load behind the rectifier circuit. Often, two smaller smoothing capacitors are used instead of one large one. Here, a capacitor is as close as possible to the rectifier circuit and the second as close as possible to the consumer. The capacitors help to fill in the gaps in the rectified voltage.
While the voltage reaches its highest values, the capacitor is charged. When it drops below a certain level, it discharges. However, due to the rectifier circuit, it cannot send the charge back to the voltage source, but discharges it via the consumer. This is why the ripple of the input voltage is slight when it reaches the consumer – the capacitor maintains the voltage.
A properly-sized capacitor can smooth not only a sinusoidal voltage but also pulse width modulation (PWM). If the capacitor chosen is too small, it does not smooth the voltage fully, and a high residual ripple remains. This can affect the functions of consumers or even cause damage. On the other hand, if the capacitor is too large, its large charging current can destroy the diodes for rectification or overload the cables.
Polarity at the smoothing capacitor
Polarity is important for many components of DC technology to ensure smooth functioning. Some devices simply will not work if they are connected with the wrong polarity, while others will be damaged. “Normal” capacitors are among the less sensitive components and can usually be connected in both directions.
But beware: The frequently used electrolytic capacitor, short Elco, is sensitive to a wrong connection. It has an oxide layer between the plates, which is designed only for the flow of current in one direction. If it is connected upside down, this layer dissolves and the capacitor becomes low impedance. Even if it is connected with a voltage well below its dielectric strength, the effect occurs with a time delay. After removing the oxide layer, the current increases and the electrolytic capacitor explodes!
Smoothing capacitor circuit design
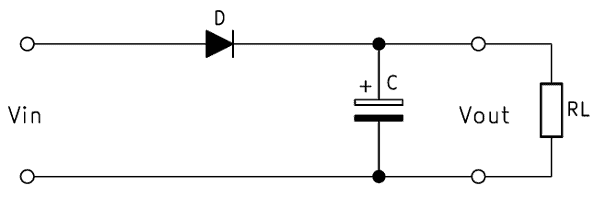
In the first circuit diagram, the smoothing capacitor is behind the half-wave rectification.
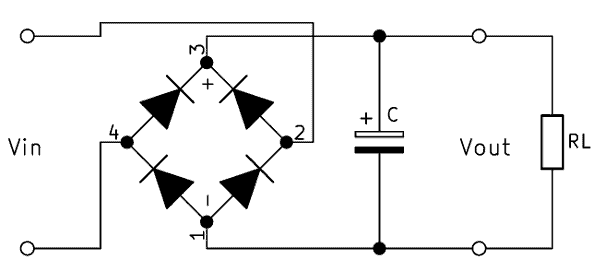
In the second circuit diagram, the smoothing capacitor is located behind the bridge rectification.
Calculate smoothing capacitor – formula
The most important formula for calculating the smoothing capacitor is:
$$ C = I \cdot \frac{\Delta t}{\Delta U} $$
The smoothing capacitor formula, alternatively:
$$ I = C \cdot \frac{\Delta U}{\Delta t} $$
Clarification:
$C$ = capacity of the capacitor in μF
$I$ = Charge current in mA
$\Delta t$ = half-period in ms
$\Delta U$ = ripple voltage in V
Explanation – Calculate smoothing capacitor
The current consumption $\mathbf{I}$ of the circuit can be calculated by Ohm’s law. A high current consumption of the consumer increases the required capacity of the capacitor enormously.
The half period $\mathbf{\Delta t}$ can be calculated from the frequency of the voltage. The formula is: $\Delta t = \frac{1}{2} \cdot T$. At the mains voltage of 50 Hz we get $\frac{1}{2} \cdot \frac{1}{50}$ with a result of $\Delta t = 10ms$.
The ripple voltage $\mathbf{ \Delta U}$ (factors in ripple voltage calculation) is the residual ripple of the voltage. Here, the type of consumer determines how far the voltage may drop. The lower the ripple voltage may fall, the larger the dimensions of the smoothing capacitor would have to be. For example, when operating LEDs, there should be no large fluctuations.
The capacitance of the smoothing capacitor $\mathbf{C}$ is our desired result in microfarad. It should also be ensured that the capacitor is designed for the corresponding voltage level. This may be interpreted broadly. An 18 V capacitor is easy to operate on a 12 V circuit.
Smoothing capacitor calculator tool
The capacitor size calculator available online helps you to calculate a smoothing capacitor. Simply enter the values using the formula described above to calculate the size you need.
Areas of application – Smooth voltage with capacitor
When converting capacitor circuits, caution is always required. Due to the charge storage in the capacitor, a large portion of the operating voltage can remain in the circuit after it’s switched off. Although it has a very low capacity compared to a battery, it is short-circuited enough to destroy components.
Probably the most widely used application of smoothing capacitors is the construction of power supplies. Regardless of the frequency with which the input voltage is applied, a capacitor is used in order to reduce the remaining resistance after rectification. Depending on the power supply, the smoothing capacitor is combined with other circuits here.
Frequency converters and other digitally operating components often produce an AC voltage via the pulse width modulation (PWM). The voltage is switched on and off periodically over different intervals. Many consumers work with PWM as with normal AC voltage. With a smoothing capacitor, the voltage of PWM can also be smoothed so that we get a DC voltage with low residual ripple at the output.